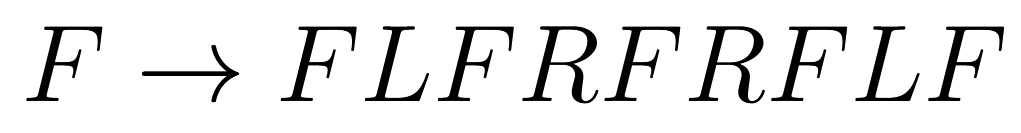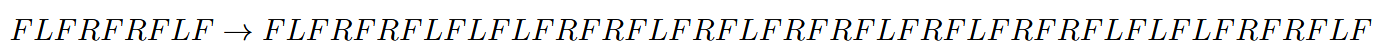Die JavaKara Umgebung
JavaKara ist eine Erweiterung der standard Kara-Umgebung in der die Zustände, durch die sich Kara steuern lässt, durch Java-Code ersetzt wurden. Das Standardprogramm, das als Template dient sieht wie folgt aus:
import javakara.JavaKaraProgram;
/* BEFEHLE: kara.
* move() turnRight() turnLeft()
* putLeaf() removeLeaf()
*
* SENSOREN: kara.
* treeFront() treeLeft() treeRight()
* mushroomFront() onLeaf()
*/
public class FindeBaum extends JavaKaraProgram {
// hier können Sie eigene Methoden definieren
public void myProgram() {
// hier kommt das Hauptprogramm hin, zB:
while (!kara.treeFront()) {
kara.move();
}
}
}
Das Programm besteht aus dem import-Statement, welches die JavaKaraProgram-Klasse in dieses Programm einbindet, das ermöglicht es uns die im unteren Kommentar stehenden Befehle zu verwenden und auf die Objekte kara, world und tools zuzugreifen. Wir können in der Programmierung mit Java also folgende Befehle verwenden:
Hinweis zu den Rückgabetypen
Die Rückgabetypen der meisten Befehle sind vom Typ
boolean, dies hängt mit der internen Fehlerbehandlung von JavaKara zusammen und in fast jedem Fall können wir hier nur einentrueWert erwarten, da einfalseWert einen Fehler wirft. Methoden die einen Fehler werfen, wurden in ihrem Rückgabetyp mit!markiert. Beispiel: Wenn vor Kara ein Baum steht undkara.move()ausgeführt wird, dann gibt diese Methodefalsezurück, diesen Wert können wir jedoch nicht verwenden, da das Programm davor mit einem Fehler beendet wird, da Kara gegen einen Baum gelaufen ist.
| Befehl | Funktion | Rückgabetyp |
|---|---|---|
kara.move() | Kara bewegt sich ein Feld nach vorne. | !boolean |
kara.turnRight() | Kara dreht sich um $90^{\circ}$ nach rechts. | !boolean |
kara.turnLeft() | Kara dreht sich um $90^{\circ}$ nach links. | !boolean |
kara.putLeaf() | Kara setzt auf das Feld, auf dem er sich gerade befindet ein Blatt. | !boolean |
kara.removeLeaf() | Kara entfernt ein Blatt auf dem Feld auf dem er sich gerade befindet. | !boolean |
kara.treeFront() | Erkennt ob ein Baum vor Kara steht. | boolean |
kara.treeRight() | Erkennt ob ein Baum rechts neben Kara steht. | boolean |
kara.treeLeft() | Erkennt ob ein Baum links neben Kara steht. | boolean |
kara.mushroomFront() | Erkennt ob ein Pilz vor Kara steht. | boolean |
kara.onLeaf() | Erkennt ob sich Kara auf einem Blatt befindet. | boolean |
Das waren die wichtigsten Methoden, die man für das Lösen der meisten Aufgaben benötigt, es gibt noch weitere die für fortgeschrittenere Programme benötigt werden, diese sind in Appendix A zu finden.
TODO!
Übersicht
In diesem Kapitel werden alle in JavaKara selbst vorhandenen Aufgaben behandelt. Es wird empfohlen, dass jeder Schüler die Aufgaben eigenhändig versucht und sich dabei mindestens 15 Minuten für die einfachen und ca. eine Stunde für die mittelschweren und schweren Aufgaben nimmt, bevor die in diesem Kapitel angesprochenen Lösungen in Augenschein genommen werden. Es wird jede Aufgabe in einem separaten Unterkapitel behandelt. Bei Bedarf wird eine Hilfestellung oder zusätzliche Information zum Problem geboten.
Neben jedem Problem steht eine subjektive Einschätzung meinerseits, wie schwierig die einzelnen Probleme zu lösen sind. Da alle Probleme außerhalb der Kategorie „Einfache Probleme“ mehr oder weniger unabhängig voneinander sind, ist es natürlich auch erlaubt, sie nach ihrer Schwierigkeit und nicht nach ihrer Auflistung zu bearbeiten. Die Reihenfolge, in der sie bearbeitet werden, bleibt natürlich dem Schüler überlassen, es sei denn, sie wird vom Lehrer vorgegeben.
Einfache Probleme
- Kara und die Blätter (2/10)
- Kara, der Tunnelsucher I. (1/10)
- Kara, der Tunnelsucher II. (2/10)
- Kleeblattsuche im Wald I. (3/10)
- Kleeblattsuche im Wald II. (4/10)
- Kleeblattsuche im Wald III. (5/10)
Mittelschwere Probleme
- Kleeblatt-PacMan (7/10)
- Wand "entlang" (4/10)
- Slalom (6/10)
- Bilder invertieren (6/10)
- Spiralen zeichnen (4/10)
- Dreiecke zeichnen (6/10)
Schwierige Probleme
- Labyrinthe (8/10)
Ab hier wird es gottlos
- Game Of Life (9/10)
- Lindenmayer-Systeme (8/10)
- Kleeblattbalken sortieren (7/10)
- Mandelbrot-Fraktal (10/10)
Aufgabenstellung
Schreiben Sie ein Programm, das Kara bis zum nächsten Baum führt. Liegt auf einem Feld ein Blatt, soll Kara es aufnehmen; liegt auf einem Feld kein Blatt, eines hinlegen. Bei dem Baum angekommen ist das Programm zu beenden.
Voraussetzungen
Wir starten jedes JavaKara Programm fürs erste mit einer leeren Hauptmethode und arbeiten uns dann Stück für Stück durch das Problem durch. Die ersten Probleme sind noch relativ trivial, werden jedoch im Verlauf des Kurses deutlich komplexer und erfordern verschiedene Problemlösestrategien.
import javakara.JavaKaraProgram;
public class Main extends JavaKaraProgram {
public static void main(String[] args) {
new Main().run("F:\\WorldOne.world");
}
public void myMainProgram() {
}
}
Hinweis
Da der Quellcode, den wir in die
myMainProgram()-Methode schreiben sofort ausgeführt wird, sobald wir aus IntelliJ das Programm starten, bleibt uns keine Zeit mehr die Welt in der JavaKara UI zu laden. Aus diesem Grund kann die.run()-Methode einen Pfad zu einer.world-Datei als optionalen Parameter erhalten. Die Welt wird dann geladen bevor das Programm ausgeführt wird.
Dieses Problem lässt sich in zwei kleinere Probleme unterteilen, zunächst müssen wir Kara nach vorne bewegen, bis er auf einen Baum stößt.
public void myMainProgram() {
while (!kara.treeFront()) {
kara.move();
}
}
Mit dem Sensor kara.treeFront() erhalten wir auskunft darüber, ob sich vor Kara ein Baum befindet. Der !-Operator ist der Negationsoperator, der einen booleschen Ausdruck negiert, d.h. in diesem Kontext, dass die while-Schleife so lange ausgeführt wird, bis kara.treeFront() den Wert true zurückgibt.
Wir könnten auch als Äquivalenten code folgendes schreiben:
public void myMainProgram() {
while (kara.treeFront() == false) {
kara.move();
}
}
Als nächstes müssen wir dafür sorgen, dass Kara ein Blatt immer dann hinlegt, wenn er auf keinem steht, und umgekehrt.
public void myMainProgram() {
while (!kara.treeFront()) {
if (kara.onLeaf()) {
kara.removeLeaf();
} else {
kara.putLeaf();
}
kara.move();
}
}
Dieser Code funktioniert im Grunde korrekt, jedoch gibt es einen Grenzfall (Edge-Case) den es zu beachten gibt: Die Ausführung der while-Schleife wird sofort unterbrochen, sobald vor Kara ein Baum erkannt wird, d.h. Dass Kara keine Chance hat das innere if-Statement auszuführen wenn sie schon vor einem Baum steht.
Das Problem lässt sich jedoch trivial lösen in dem wir einfach das if-Statement ein weiteres mal wiederholen.
public void myMainProgram() {
while (!kara.treeFront()) {
if (kara.onLeaf()) {
kara.removeLeaf();
} else {
kara.putLeaf();
}
kara.move();
}
if (kara.onLeaf()) {
kara.removeLeaf();
} else {
kara.putLeaf();
}
}
Um den Code etwas schöner zu gestalten und um das DRY-Prinzip (Don't Repeat Yourself) einzuhalten, können wir dieses if-Statement in eine weitere Methode auslagern und diese stattdessen aufrufen.
public void myMainProgram() {
while (!kara.treeFront()) {
this.invertLeaf();
kara.move();
}
this.invertLeaf();
}
private void invertLeaf() {
if (kara.onLeaf()) {
kara.removeLeaf();
} else {
kara.putLeaf();
}
}
Aufgabenstellung
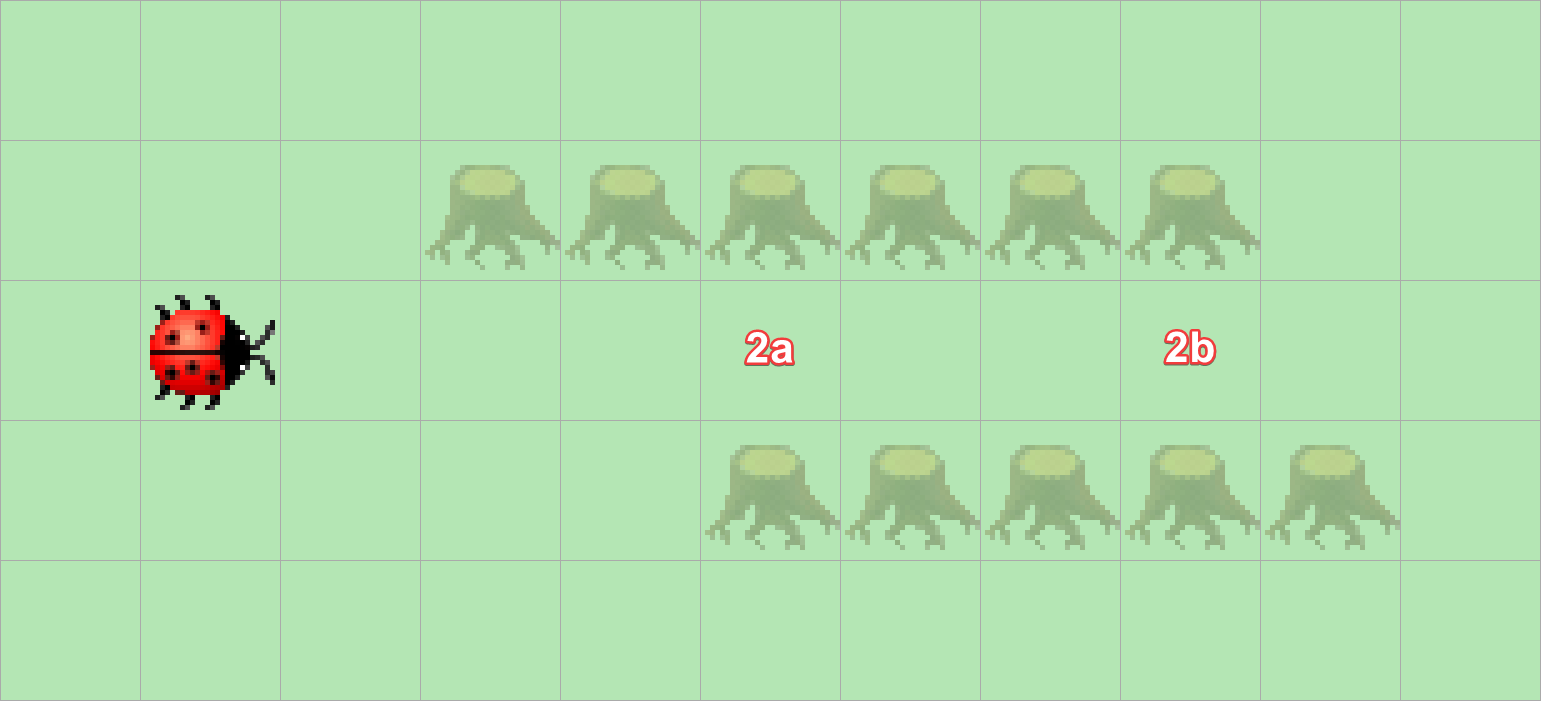
Kara sucht den Eingang eines geraden Tunnels (Feld 2a). Schreiben Sie ein Programm, das ihn auf dem ersten Feld im Tunnelinnern anhalten lässt. Aber Achtung: manche Tunnels haben zunächst eine einseitige Wand, manche links, manche rechts.
Zur Lösung dieses Problems benötigen wir zwei andere Sensoren. Anstelle von kara.treeFront() benötigen wir kara.treeRight() und kara.treeLeft(), diese kombinieren wir wieder mit einer while-Schleife, da Kara so lange nach vorne laufen soll, bis er sowohl links als auch rechts von sich einen Baum stehen hat.
Dieses Problem führt auch den logischen UND-Operator ein, der in Java mit && implementiert ist.
public void myMainProgram() {
while (!(kara.treeLeft() && kara.treeRight())) {
kara.move();
}
}
Ausdrücke (Expressions) befolgen die gleichen Regeln wie die arithmetischen Operatoren in der Mathematik. D.h. hier, dass zuerst der Ausdruck kara.treeLeft() && kara.treeRight() evaluiert wird, dieser gibt dann anhand der folgenden Wahrheitstabelle einen Wert zurück, der dann von dem !-Operator außerhalb der Klammern negiert wird.
kara.treeLeft() | kara.treeRight() | kara.treeLeft() && kara.treeRight() | !(kara.treeLeft() && kara.treeRight()) |
|---|---|---|---|
false | false | false | true |
false | true | false | true |
true | false | false | true |
true | true | true | false |
Aus dieser Tabelle lässt sich auch gut entnehmen, dass unser Program nur dann hält, wenn Kara am Tunneleingang steht.
Aufgabenstellung
Kara will den Ausgang des Tunnels finden (Feld 2b). Dazu muss er zunächst den Tunnel durchqueren. Schreiben Sie ein Programm, das ihn auf dem ersten Feld nach dem Tunnel anhalten lässt – er soll nicht bis zum Ende der Gallerie laufen!
Für dieses Programm muss Kara erstmal in den Tunnel hinein, dafür können wir den vorherigen Code verwenden. Um dann aus dem Tunnel herauszufinden können wir diesen Code erneut anwenden, jedoch negieren.
public void myMainProgram() {
while (!(kara.treeLeft() && kara.treeRight())) {
kara.move();
}
while (kara.treeLeft() && kara.treeRight()) {
kara.move();
}
}
Hinweis
Viele logische Verbindungen folgen aus der Aussagenlogik, die mitunter des Morganschen Gesetzes in fast jeder Mathematikvorlesung zur Mengenlehre aufzufinden sind. Da sie die Grundlagen der formalen Sprache bilden. Wenn wir
!(kara.treeLeft() && kara.treeRight())negieren, erhalten wir eigentlich!(!(kara.treeLeft() && kara.treeRight())), dies ist aber gleichwertig mitkara.treeLeft() && kara.treeRight()da sich doppelte Negationen auflösen, dies lässt sich ebenfalls wieder an einer Wahrheitstabelle trivial ablesen.
Bedingung !Bedingung !(!Bedingung) falsetruefalsetruefalsetrueWer sich für ein Informatik- oder Mathematikstudium interessiert, sollte sich mit der Aussagenlogik vertraut machen.
Aufgabenstellung
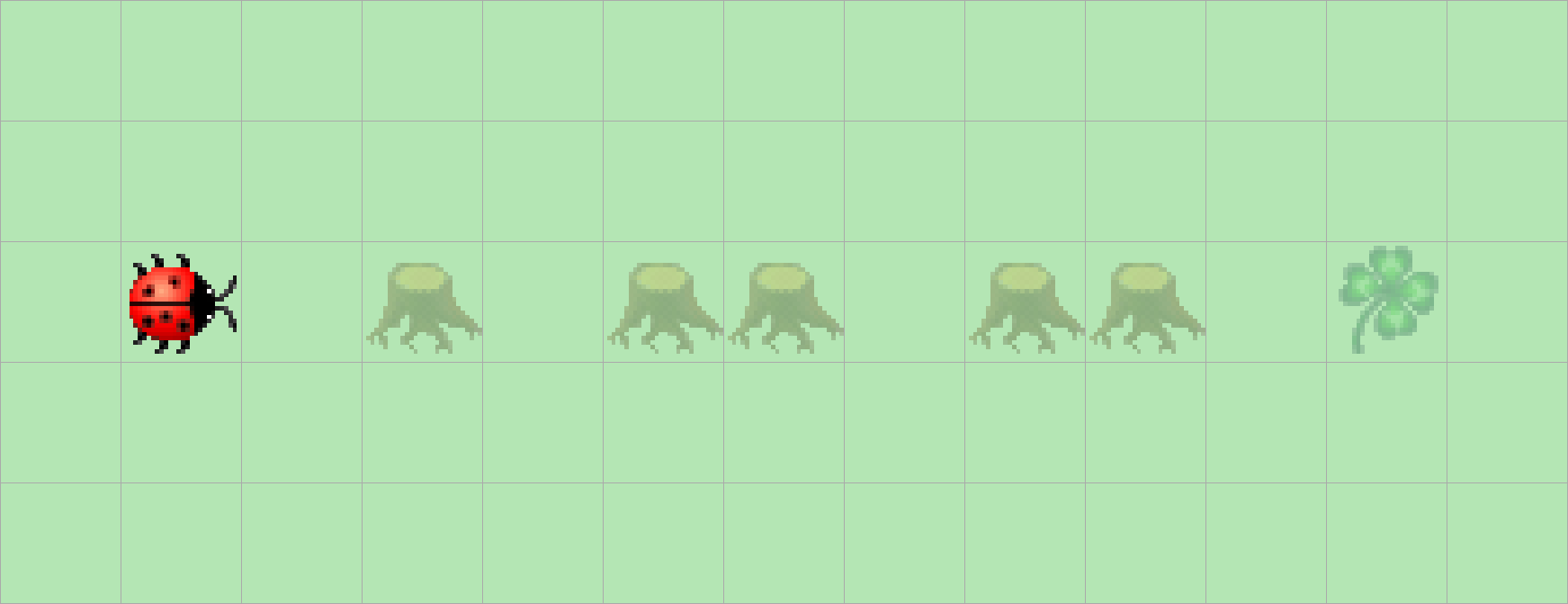
Kara sucht ein Kleeblatt. Er weiss, dass eines geradeaus vor ihm liegt - er muss nur um die Bäume herumlaufen. Glücklicherweise stehen nie zwei Bäume nebeneinander. Schreiben Sie ein Programm, das ihn bis zum Kleeblatt führt!
Diese Aufgabe ist im Vergleich zu den vorherigen schon etwas komplexer, wir benötigen eine Bedingung, die das Programm zu halten bringt, eine Methode mit der wir die Bäume umgehen können und eine Bedingung um diese Methode aufzurufen.
Wir wissen, dass das Ziel erreicht wurde, wenn Kara auf dem Kleeblatt steht, dafür haben wir die Methode kara.onLeaf().
public void myMainProgram() {
while (!kara.onLeaf()) {
}
}
Wenn ein Baum vor Kara steht, muss dieser umgangen werden, ansonsten muss Kara geradeaus laufen.
public void myMainProgram() {
while (!kara.onLeaf()) {
if (kara.treeFront()) {
this.bypassTree();
} else {
kara.move();
}
}
}
Die bypassTree()-Methode besteht aus hartkodierten Anweisungen. Hartkodierung bedeutet, dass eine oder mehrere Anweisungen, Werte oder Definitionen fest in den Programmcode integriert wurden und sich nicht aus einer, vom Code selbst herausgehenden Algorithmik ergeben.
private void bypassTree() {
kara.turnLeft();
kara.move();
kara.turnRight();
kara.move();
kara.move();
kara.turnRight();
kara.move();
kara.turnLeft();
}
Aufgabenstellung
Erweitern Sie Ihr Programm aus Aufgabe 4 so, dass Kara auch mit mehreren nebeneinander stehenden Bäumen fertig wird!
Hier können wir ebenfalls den Code aus Aufgabe 4 als Grundlage verwenden, wir müssen nur die bypassTree()-Methode um etwas Logik erweitern.
private void bypassTree() {
kara.turnLeft();
kara.move();
kara.turnRight();
do {
kara.move();
} while (kara.treeRight());
kara.turnRight();
kara.move();
kara.turnLeft();
}
Hier verwenden wir eine Abwandlung der while-Schleife, die do-while-Schleife genannt wird, sie ist Fußgesteuert, d.h. die Bedingung ist am Ende der Instruktionen angesiedelt und deshalb werden die Instruktionen auch mindestens einmal ausgeführt, selbst wenn die eigentliche Bedingung nicht erfüllt ist, die do-while-Schleife hier ist Äquivalent zu:
private void bypassTree() {
// ...
kara.move();
while (kara.treeRight()) {
kara.move();
}
// ...
}
Die Hauptmethode bleibt unverändert.
Aufgabenstellung
In Karas Welt gibt es Wälder mit Rundgängen, in denen Kara auf Kleeblättersuche geht. Jedes Feld in einem Rundgang hat genau zwei freie benachbarte Felder. Eines davon liegt hinter Kara, von diesem Feld aus ist auf das aktuelle Feld gekommen.
Für diese Aufgaben starten wir wieder mit einer neuen Hauptfunktion, jedoch können wir die Abbruchbedingung beibehalten.
public void myMainProgram() {
while (!kara.onLeaf()) {
}
}
Um Kara durch diesen "Wald" zu navigieren benötigen wir alle drei Baumsensoren kara.treeFront(), kara.treeRight() und kara.treeLeft(). Anhand der Struktur des Waldes können wir erkennen, dass immer nur einer dieser drei Sensoren den Wert false zurückgibt, an diesen können wir uns dann orientieren und Kara dorthin bewegen.
public void myMainProgram() {
while (!kara.onLeaf()) {
if (!kara.treeFront()) {
// Wenn kein Baum vor Kara ist, dann nach vorne bewegen.
kara.move();
} else if (!kara.treeRight()) {
// Wenn ein Baum vor Kara ist, jedoch kein Baum rechts nebem Kara, dann nach rechts bewegen.
kara.turnRight();
kara.move();
} else {
// Wenn ein Baum vor Kara und rechts neben Kara ist, dann nach links bewegen.
kara.turnLeft();
kara.move();
}
}
}
Aufgabenstellung
Programmieren Sie Kara so, dass er die Spur von Kleeblättern "auffrisst"! Da Sie wissen, dass die Spur nie entlang eines Baumes geht, kann das Programm beendet werden, sobald Kara auf einem Kleeblatt vor einem Baum steht. Sie können selbst bestimmen, ob Sie auf einem Kleeblatt oder davor starten wollen.

In der Aufgabenstellung wurde uns bereits die Bedingung gegeben, dass das Programm halten soll, sobald Kara vor einem Baum steht, dies können wir als unsere Hauptschleife verwenden.
public void myMainProgram() {
while (!kara.treeFront()) {
}
}
Innerhalb der Schleife müssen wir nun prüfen ob sich Kara auf einem Blatt befindet, wenn das der Fall ist, dann soll Kara das Blatt aufheben und weiterlaufen.
public void myMainProgram() {
while (!kara.treeFront()) {
if (kara.onLeaf()) {
kara.removeLeaf();
kara.move();
}
}
}
Falls Kara zu weit läuft und kein Blatt mehr unter Kara liegt, können wir umdrehen und eine andere Route einschlagen.
public void myMainProgram() {
while (!kara.treeFront()) {
if (kara.onLeaf()) {
kara.removeLeaf();
kara.move();
if (!kara.onLeaf()) {
this.turnAround();
this.checkSurroundings();
}
}
}
}
turnAround() ist eine ziemlich selbsterklärende Methode
private void turnAround() {
kara.turnLeft();
kara.turnLeft();
kara.move();
}
die Magie dieses Algorithmus steckt eher in checkSurroundings(), da ich mich entschieden habe ein etwas fortgeschritteneres Konzept der Informatik und Mathematik zu verwenden: Rekursion.
private void checkSurroundings() {
kara.turnRight();
kara.move();
if (!kara.onLeaf()) {
this.turnAround();
this.checkSurroundings(); // Rekursiver Methodenaufruf
}
}
Zunächst bewegt sich Kara wieder nach rechts, dann wird geprüft ob Kara dieses mal auf einem Blatt steht, ist dies wieder nicht der Fall, dreht sich Kara wieder um, geht zurück und ruft die checkSurroundings()-Methode aus dem inneren dieser Methode selbst auf.
Informelle Definition von Rekursion
Rekursion ist der Prozess, den eine Prozedur durchläuft, wenn einer der Schritte der Prozedur den Aufruf der Prozedur selbst beinhaltet. Eine Prozedur, die eine Rekursion durchläuft, wird als „rekursiv“ bezeichnet. Ein Beispiel für Rekursion bietet die Fibonacci-Folge, die wie folgt gebildet wird: Sei \( F(0) = 0 \) und \(F(1) = 1\), dann gilt für alle \(n \in \mathbb{N}\) mit \(n > 1\), dass \[F(n) = F(n - 1) + F(n - 2)\] Daraus ergibt sich die Folge \[ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ... \]
Aufgabenstellung
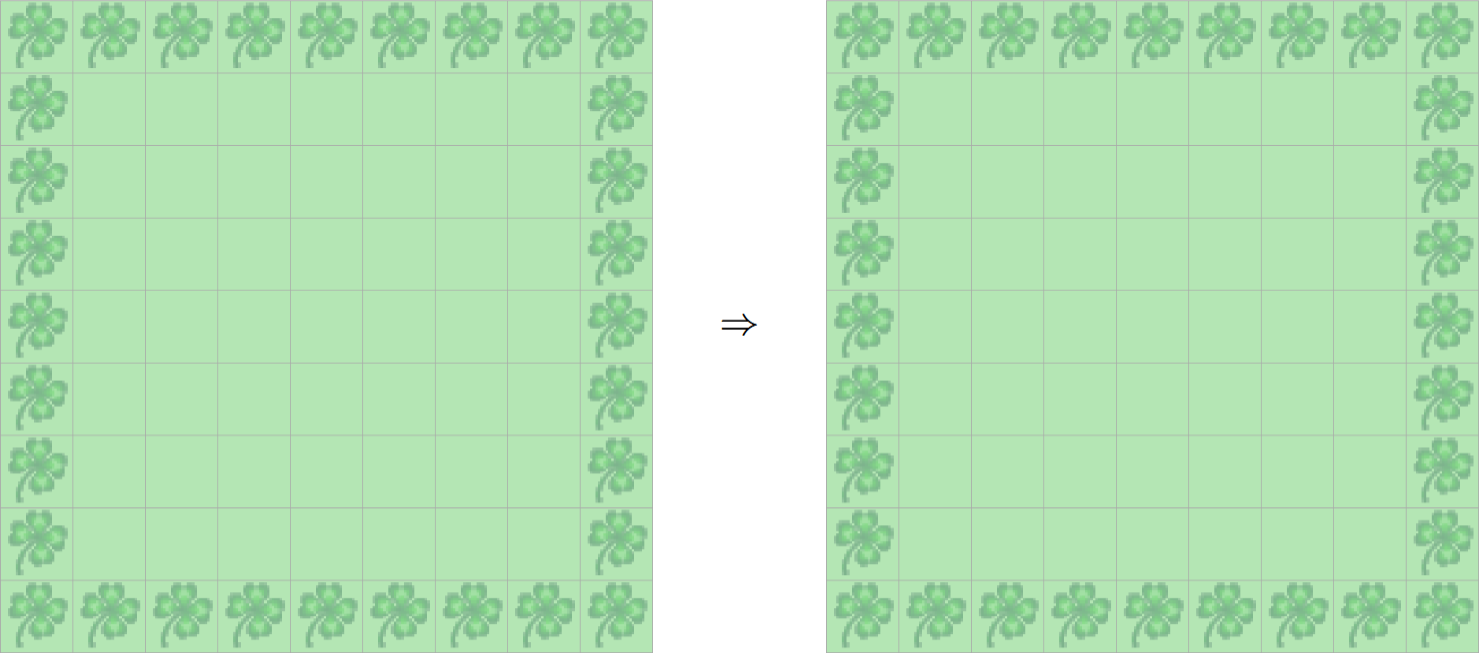
Kara möchte einen Wald im Uhrzeigersinn patrouillieren. Programmieren Sie Kara so, dass er endlos im Uhrzeigersinn um diesen Wald läuft.
Da Kara sich im Uhrzeigersinn bewegen soll, benötigen wir nur kara.treeFront() und kara.treeRight().
Da unser Code unendlich lange laufen soll, verwenden wir eine while-true-Schleife.
public void myMainProgram() {
while (true) {
}
}
Wir haben zwei Sensoren, die wir prüfen müssen, erstmal
public void myMainProgram() {
while (true) {
if (!kara.treeFront()) {
} else {
}
}
}
und
public void myMainProgram() {
while (true) {
if (!kara.treeFront()) {
if (kara.treeRight()) {
} else {
}
} else {
}
}
}
Ich habe mich dazu entschieden, den Code so zu schreiben, anstatt die beiden Bedingungen mit einem logischen UND zu verknüpfen. So ist er lesbarer und es ist einfacher, die einzelnen Pfade nachzuvollziehen. Wenn ein Baum vor Kara steht, drehen wir uns nach links. Steht kein Baum vor Kara, müssen wir zusätzlich prüfen, ob rechts neben Kara ein Baum steht. Steht dort ein Baum, können wir einfach weiterlaufen. Steht dort kein Baum, müssen wir nach rechts gehen.
public void myMainProgram() {
while (true) {
if (!kara.treeFront()) {
if (kara.treeRight()) {
kara.move();
} else {
kara.turnRight();
kara.move();
}
} else {
kara.turnLeft();
}
}
}
Die von den JavaKara-Erstellern vorgeschlagene Lösung für dieses Problem ist falsch und führt in Welt Zwei zu einer Endlosschleife.
public void myMainProgram() {
while (true) { // laufe endlos den Bäumen entlang
if (kara.treeFront() && kara.treeRight()) { // vorne und rechts ein Baum?
kara.turnLeft(); // Linksdrehung!
} else if (!kara.treeFront()) { // vorne kein Baum?
if (kara.treeRight()) { // rechts ein Baum?
kara.move(); // Schritt vorwärts!
} else { // rechts kein Baum
kara.turnRight(); // Rechtsdrehung und
kara.move(); // Schritt vorwärts
}
}
}
}
Aufgabenstellung
Kara möchte zwischen den Bäumen Slalom fahren. Programmieren Sie Kara so, dass er den Slalom endlos hin- und zurück fährt. Am Anfang ist Kara immer so platziert, dass er zuerst eine Linkskurve machen muss. Wie lange der Parcour ist (wieviele Bäume der Slalom hat), weiss Kara zu Beginn natürlich nicht. Es soll ihm auch egal sein, ob die Bäume horizontal oder vertikal nebeneinander stehen.
Um dieses Problem zu lösen, müssen wir die Zustände, in denen sich Kara befinden kann, genau betrachten. Anhand der vorherigen Drehung müssen wir dann entscheiden, ob wir uns nach rechts oder nach links drehen sollen. Um eine Art „Schalter” zu programmieren, der jedes Mal umgeschaltet wird, sobald Kara sich bewegt, eignet sich ein boolean am besten, da dieser nur zwei Werte annehmen kann (true oder false). Unser Hauptprogramm befindet sich wieder in einer Endlosschleife. Wir prüfen zunächst die beiden Zustände, die für das Umkehren im Slalom verantwortlich sind: Steht links neben Kara ein Baum, rechts jedoch nicht, dann drehen wir uns nach links. Steht rechts neben Kara ein Baum, links jedoch nicht, drehen wir uns nach rechts. Solange Kara zwischen zwei Bäumen steht, soll er hin und her laufen.
public void myMainProgram() {
boolean lastMoveLeft = false;
while (true) {
if (kara.treeLeft() && !kara.treeRight()) {
this.aroundTreeLeft();
lastMoveLeft = true;
} else if (!kara.treeLeft() && kara.treeRight()) {
this.aroundTreeRight();
lastMoveLeft = false;
}
while (kara.treeLeft() && kara.treeRight()) {
if (lastMoveLeft) {
this.aroundTreeRight();
lastMoveLeft = false;
} else {
this.aroundTreeLeft();
lastMoveLeft = true;
}
}
}
}
private void aroundTreeLeft() {
kara.move();
kara.turnLeft();
kara.move();
kara.move();
kara.turnLeft();
kara.move();
}
private void aroundTreeRight() {
kara.move();
kara.turnRight();
kara.move();
kara.move();
kara.turnRight();
kara.move();
}
Aufgabenstellung
Programmieren Sie Kara so, dass er ein "Negativbild" von dem Kleeblattbild innerhalb des Baumrechtecks erstellt. Wo ein Kleeblatt liegt, soll er es aufnehmen, und wo keines liegt, soll er eines hinlegen. Kara startet immer oben links in der Ecke mit Blick nach rechts.
TODO! EXPLAIN LATER
boolean exit = false;
public void myMainProgram() {
boolean lastSwitchLeft = true;
while (!exit) {
if (!kara.treeFront()) {
this.invert();
kara.move();
} else {
this.invert();
if (lastSwitchLeft) {
this.nextRowRight();
lastSwitchLeft = false;
} else {
this.nextRowLeft();
lastSwitchLeft = true;
}
}
}
}
private void invert() {
if (kara.onLeaf()) {
kara.removeLeaf();
} else {
kara.putLeaf();
}
}
private void nextRowRight() {
kara.turnRight();
if (kara.treeFront()) {
exit = true;
return;
}
kara.move();
kara.turnRight();
}
private void nextRowLeft() {
kara.turnLeft();
if (kara.treeFront()) {
exit = true;
return;
}
kara.move();
kara.turnLeft();
}
Aufgabenstellung
Programmieren Sie Kara so, dass er eine Kleeblatt-Spirale wie die obige zeichnet. Von innen nach aussen ist jede Kante der Spirale um eins länger als die vorangehende.
TODO!
public void myMainProgram() {
int counter = 1;
int limit = 19;
while (counter <= limit) {
for (int i = 0; i < counter; i++) {
kara.putLeaf();
kara.move();
}
kara.turnRight();
counter++;
}
}
Aufgabenstellung
Programmieren Sie Kara so, dass er Dreiecke zeichnet!
Erklärung der Lösungen zum Zeichnen von Dreiecken
Kara zeichnet aufsteigende Dreiecke, indem er Blätter in sich vergrößernden Reihen platziert. Beide Lösungen nutzen eine Schleifenstruktur, um die Dreiecksform schrittweise aufzubauen, unterscheiden sich aber in der Effizienz der Bewegungen.
Lösung 1 (Simpel)
Kara bewegt sich in rechteckigen Schleifen und verdoppelt die Schritte pro Ebene.
public void myMainProgram() {
int counter = 1;
while (counter <= 10) {
// Zeichnet eine waagerechte Linie mit Blättern
for (int i = 0; i < counter; i++) {
kara.putLeaf();
kara.move();
}
// Dreht nach rechts und bewegt sich zur nächsten Reihe
kara.turnRight();
kara.move();
kara.turnRight();
counter++;
// Bewegt sich zurück, ohne Blätter zu legen
for (int i = 0; i < counter; i++) {
kara.move();
}
// Dreht erneut um, um die nächste Linie zu starten
kara.turnRight();
kara.turnRight();
counter++;
}
}
Schritt-für-Schritt:
- Waagerechte Linie: Kara legt
counter-viele Blätter und bewegt sich vorwärts. - Rechtsabbiegung: Dreht nach rechts, bewegt sich eine Position nach oben (neue Reihe).
- Rückweg: Bewegt sich
counter + 1Schritte zurück (ohne Blätter). - Neue Linie vorbereiten: Dreht um 180°, um in die entgegengesetzte Richtung zu blicken.
- Vergrößerung: Der
counterwird pro Schleifendurchlauf zweimal erhöht, sodass jede neue Linie länger wird.
Effekt:
Kara zeichnet ein rechteckiges Spiralmuster, das sich zu Dreiecken formt. Die Bewegung ist jedoch nicht optimiert, da er leere Wege zurücklegt (z. B. beim Rückweg ohne Blätter).
Lösung 2 (Schneller)
Kara nutzt abwechselnde Links-/Rechtsdrehungen, um direkter zur nächsten Reihe zu gelangen.
public void myMainProgram() {
int counter = 1;
boolean turnedLeft = true;
while (counter <= 10) {
// Zeichnet eine waagerechte Linie mit Blättern
for (int i = 0; i < counter; i++) {
kara.putLeaf();
kara.move();
}
// Abwechselnd nach rechts oder links drehen
if (turnedLeft) {
kara.turnRight();
kara.move();
kara.turnRight();
turnedLeft = false;
} else {
kara.turnLeft();
kara.move();
kara.turnLeft();
turnedLeft = true;
}
counter += 2; // Größere Sprünge pro Ebene
}
}
Schritt-für-Schritt:
- Waagerechte Linie: Wie in Lösung 1 legt Kara
counter-viele Blätter. - Abwechselnde Drehung:
- Rechtsabbiegung: Nach der ersten Linie dreht Kara rechts, bewegt sich nach oben, dreht erneut rechts (blickend in die Gegenrichtung).
- Linksabbiegung: In der nächsten Ebene dreht er links, bewegt sich nach oben, dreht erneut links.
- Effiziente Positionierung: Durch die alternierenden Drehungen spart Kara leere Rückwege und bewegt sich direkt zur nächsten Startposition.
- Schnelleres Wachstum: Der
counterwird pro Durchlauf um 2 erhöht, was weniger Schleifendurchläufe erfordert.
Effekt:
Kara zeichnet das Dreieck direkter und schneller, da er keine redundanten Bewegungen ausführt. Das Muster entsteht durch abwechselndes Rechts-/Links-Wenden, was eine optimierte Pfadführung ermöglicht.
Gemeinsamkeiten & Unterschiede
| Aspekt | Lösung 1 | Lösung 2 |
|---|---|---|
| Bewegung | Immer rechtsdrehend, leere Wege | Abwechselnd rechts/links, direkt |
| Counter-Update | +1 pro Teilbewegung (insb. +2) | +2 pro Schleife |
| Effizienz | Langsamer (mehr Schritte) | Schneller (optimierter Pfad) |
| Muster | Spiralförmig | Direktes Dreieck |
Visualisierung:
Stell dir vor, Kara läuft zuerst wie eine Zick-Zack-Linie (Lösung 2) oder eine sich aufblähende Spirale (Lösung 1), wobei jede Linie länger wird, bis das Dreieck vollständig ist.
Aufgabenstellung
Führen Sie Kara durch das Labyrinth zum Kleeblatt. Jede horizontale Baumreihe, ausser der untersten, hat genau einen Ausgang, der in die nächst höhere Zeile führt. Diesen muss Kara jeweils finden. Hinter dem letzten Ausgang wartet das Kleeblatt auf ihn. Programmieren Sie Kara so, dass er das Kleeblatt findet und aufnimmt. Dabei soll er nie an einem Ausgang vorbeilaufen, ohne ihn zu benutzen! Zu Beginn schaut Kara immer nach rechts.
Verbesserte Erklärung des Codes:
Kara navigiert durch das Labyrinth mithilfe der "Rechte-Hand-Regel": Er folgt stets der rechten Wand, um den Ausgang jeder Baumreihe zu finden. Jede horizontale Reihe (außer der untersten) hat genau einen Durchgang zur nächsthöheren Reihe. Der Algorithmus stellt sicher, dass Kara diesen Durchgang nie verpasst und direkt zum Kleeblatt gelangt.
Schritt-für-Schritt Ablauf:
-
Äußere Schleife: Zielerkennung
while (!kara.onLeaf())
Die Schleife läuft, bis Kara das Kleeblatt erreicht hat. -
Innere Schleife: Rechtswand folgen
while (kara.treeRight()) { ... }
Solange rechts ein Baum ist, bewegt sich Kara entlang der rechten Wand:- Blockierter Weg vorne:
Sind rechts und vorne Bäume (Sackgasse), dreht Kara um (turnRight()zweimal → 180°-Wende). - Freier Weg vorne:
Ist nur rechts ein Baum, geht Kara vorwärts (move()), um der Wand weiter zu folgen.
- Blockierter Weg vorne:
-
Rechtsabbiegung: Ausgang finden
if (!kara.onLeaf()) { ... }
Sobald rechts kein Baum mehr ist (Ausgang zur nächsten Reihe):- Kara dreht nach rechts (
turnRight()), um in den Durchgang zu blicken. - Er geht einen Schritt in den Durchgang (
move()).
Die Prüfung!kara.onLeaf()verhindert, dass Kara sich nach Erreichen des Ziels unnötig bewegt.
- Kara dreht nach rechts (
Warum funktioniert das?
- Das Labyrinth ist so konstruiert, dass jede Reihe genau einen Ausgang nach oben hat.
- Durch das ständige "Rechtshalten" findet Kara garantiert den Durchgang, ohne ihn zu übersehen.
- Die letzte Bewegung zum Kleeblatt wird durch die Prüfung
!kara.onLeaf()exakt gestoppt.
Visualisierung:
Stell dir vor, Kara "streicht" mit der rechten Pfote immer an der Wand entlang. Sobald die Wand endet (rechts frei), betritt er die nächste Reihe. So windet er sich systematisch durch das Labyrinth bis zum Ziel.
public void myMainProgram() {
while (!kara.onLeaf()) {
while (kara.treeRight()) {
if (kara.treeFront()) {
kara.turnRight();
kara.turnRight();
} else {
kara.move();
}
}
if (!kara.onLeaf()) {
kara.turnRight();
kara.move();
}
}
}
Aufgabenstellung
Kara möchte dem "Game of Life" zuschauen. Ausgedacht hat sich dieses "Spiel" der amerikanische Mathematiker Conway. Die Regeln sind einfach: Ein Feld in Kara's Welt ist entweder besetzt (Kleeblatt drauf) oder unbesetzt (kein Kleeblatt drauf). Die ganze Welt kann man sich als Population von Lebewesen vorstellen, aus der sich die nächste Generation nach folgenden Regeln entwickelt:
Ein leeres Feld wird in der nächsten Generation besetzt, wenn es genau drei besetzte Nachbarfelder hat. Beispiel: Das mittlere, leere Feld hat drei besetzte Nachbarfelder und wird daher "geboren":
Ein besetztes Feld bleibt auch in der nächsten Generation besetzt, wenn es zwei oder drei besetzte Nachbarfelder hat. Beispiel: Das mittlere Feld mit Kleeblatt (hell) hat drei besetzte Nachbarfelder und bleibt daher am Leben:
Alle Felder, bei denen die Voraussetzungen der Regeln 1 und 2 nicht zutreffen, sind in der nächsten Generation unbesetzt. Beispiel: Das mittlere Feld mit Kleeblatt (hell) hat zu viele besetzte Nachbarfeldern und "stirbt" daher: Auch bei relativ einfachen Startwelten (mit vier oder fünf besetzten Feldern) ist es schwierig, die Entwicklung der nächsten Generationen vorauszusehen. Man muß sie wirklich durchspielen!
Hinweis
Auch hier ist der Lösungsansatz der in JavaKara integriert ist, eher suboptimal. Der Code
- Ignoriert Randzellen (verarbeitet nur innere Zellen von
(1,1)bis(SIZE-2, SIZE-2)). Randzellen bleiben für immer in ihrem Ausgangszustand und zerstören die Simulation.- Zählt die momentane Zelle selbst und subtrahiert 1, wenn sie noch lebt. Obwohl mathematisch gleichwertig, ist dieser Ansatz weniger intuitiv und effizient, als die momentane Zelle von der Berechnung direkt auszuschließen.
- Initialisierung von Randzellen schlägt fehl, was zu falschen Startbedingungen führt, wenn Ränder Blätter haben.
Dies wird anhand von folgendem Beispiel sehr deutlich
Es sollte jedoch so aussehen:
Der Code geht davon aus, dass die Kara-Welt nicht kontinuierlich ist, d.h. dass das Feld links von (0, 0) anstelle von (world.getSizeX() - 1, 0) nicht existiert. Die Ränder der Welt grenzen diese sozusagen vollständig ab, so dass man nicht auf der einen Seite hinausgehen und auf der anderen wieder herauskommen kann. Dies ist jedoch nur meine Annahme, die ich aufgrund der zusätzlichen und unnötigen Komplexität getroffen habe, die ansonsten erforderlich wäre, um dieses Wrapping-Verhalten zu implementieren.
Zunächst erstellen wir also einen boolean-Array, den wir verwenden um die Daten der einzelnen Zellen zu speichern, ist eine Zelle am Leben (ein Blatt liegt auf diesem Feld), dann ist der Wert für die Koordinaten des Feldes im Array true, ansonsten false.
boolean[][] field = new boolean[world.getSizeX()][world.getSizeY()];
for (int x = 0; x < field.length; x++) {
for (int y = 0; y < field[x].length; y++) {
// Da world.isLeaf() einen boolean zurückgibt, ist diese Implementierung besonders gut geeignet.
field[x][y] = world.isLeaf(x, y);
}
}
Die Hauptmethode sollte auch in einer Endlosschleife laufen, dadurch erhalten wir folgenden Code:
public void myMainProgram() {
boolean[][] field = new boolean[world.getSizeX()][world.getSizeY()];
while (true) {
// Erfassung des aktuellen Zustands
for (int x = 0; x < field.length; x++) {
for (int y = 0; y < field[x].length; y++) {
field[x][y] = world.isLeaf(x, y);
}
}
}
}
Da wir nun wissen, wie die jetzige Welt aussieht, können wir anhand dieser die nächste Iteration berechnen. Das ist der komplexe Teil des Programms.
private boolean[][] updateLife(boolean[][] field) {
boolean[][] nextIteration = new boolean[field.length][field[0].length];
for (int x = 0; x < field.length; x++) {
for (int y = 0; y < field[x].length; y++) {
int neighbors = countNeighbors(field, x, y);
nextIteration[x][y] = field[x][y] ? (neighbors == 2 || neighbors == 3) : (neighbors == 3);
}
}
return nextIteration;
}
Wir erstellen mit boolean[][] nextIteration = new boolean[field.length][field[0].length]; wieder einen neuen Array, der die Daten der nächsten Iteration halten soll, ziemlich selbsterklärend. In den darauffolgenden for-Schleifen iterieren wir wieder über jedes einzelne Feld, und mit der countNeighbors()-Methode zählen wir alle Nachbarn des Feldes mit den Koordinaten (x, y). Zu der Funktion kommen wir gleich.
Zunächst müssen wir noch klären was es sich mit
nextIteration[x][y] = field[x][y]
? (neighbors == 2 || neighbors == 3)
: (neighbors == 3);
auf sich hat. Die ? und : Symbole sind teil des ternären-Operators. Die obige Schreibweise ist eine kurzschreibweise für:
if (field[x][y]) {
nextIteration[x][y] = (neighbors == 2 || neighbors == 3);
} else {
nextIteration[x][y] = (neighbors == 3);
}
wobei dies auch wieder ausführlicher geschrieben werden kann mit
if (field[x][y]) {
if (neighbors == 2 || neighbors == 3) {
nextIteration[x][y] = true;
} else {
nextIteration[x][y] = false;
}
} else {
if (neighbors == 3) {
nextIteration[x][y] = true;
} else {
nextIteration[x][y] = false;
}
}
Übrigens, Ternär bedeutet einfach, dass der Operator mit drei Werten arbeitet.
Die einfachen arithmetischen Operatoren (+, -, *, /) sind alle binäre Operatoren, weil sie mit zwei Werten arbeiten.
Und der Negationsoperator ! ist ein unärer Operator.
Diese glorifizierte if-Anweisung prüft die Regeln des Spiels des Lebens, die in der Aufgabe definiert sind.
Kommen wir nun zu dem Teil, der in der gegebenen JavaKara-Lösung falsch gemacht wurde. Die Zählung der Nachbarn.
private int countNeighbors(boolean[][] field, int x, int y) {
int count = 0;
int xMin = Math.max(x - 1, 0);
int xMax = Math.min(x + 1, field.length - 1);
int yMin = Math.max(y - 1, 0);
int yMax = Math.min(y + 1, field[0].length - 1);
for (int i = xMin; i <= xMax; i++) {
for (int j = yMin; j <= yMax; j++) {
// Wir schließen i == x und j == y aus, weil wir sonst das Feld prüfen, dessen Nachbarn wir zählen.
if (field[i][j] && !(i == x && j == y)) {
count++;
}
}
}
return count;
}
Die Math.min und Math.max Methoden nehmen zwei Parameter als input und geben je nach Methode den größeren oder kleineren Wert zurück.
Math.min(3, 5)gibt3zurück.Math.max(3, 5)gibt5zurück.
int xMin = Math.max(x - 1, 0);
int xMax = Math.min(x + 1, field.length - 1);
int yMin = Math.max(y - 1, 0);
int yMax = Math.min(y + 1, field[0].length - 1);
Wir verwenden diese Methoden, um die Kanten und Ränder der Welt korrekt zu berechnen.
Angenommen, wir wollen die Nachbarn des Feldes (0, 0) berechnen, dann wäre xMin ohne die obigen Methoden -1 (gilt auch für yMin).
Das würde zu einem Fehler führen, sobald wir ein Blatt auf diese Koordinaten setzen, also setzen wir den Wert wieder auf 0.
Für (0, 0) prüfen wir also nur die Felder (1, 0), (0, 1) und (1, 1).
Der Rest des Codes ist eigentlich relativ einfach, wir setzen die oben genannten Variablen als unsere Schleifengrenzen und prüfen, ob es ein Blatt auf diesen Feldern gibt, zählen dann den Zähler hoch und ignorieren das Feld, dessen Nachbarn wir zu finden versuchen.
import javakara.JavaKaraProgram;
public class Main extends JavaKaraProgram {
private static final int INITIAL_SLEEP_MS = 2000;
private static final int WAIT_DURATION_MS = 125;
public static void main(String[] args) {
new Main().run("F:\\Worlds\\GameOfLife\\WorldOne.world");
}
public void myMainProgram() {
boolean[][] field = new boolean[world.getSizeX()][world.getSizeY()];
sleep(INITIAL_SLEEP_MS);
while (true) {
sleep(WAIT_DURATION_MS);
// Erfassung des aktuellen Zustands
for (int x = 0; x < field.length; x++) {
for (int y = 0; y < field[x].length; y++) {
field[x][y] = world.isLeaf(x, y);
}
}
// Berechnung der nächsten Generation
field = updateLife(field);
// Weltzustand aktualisieren
updateField(field);
}
}
private void updateField(boolean[][] field) {
for (int x = 0; x < field.length; x++) {
for (int y = 0; y < field[x].length; y++) {
world.setLeaf(x, y, field[x][y]);
}
}
}
private boolean[][] updateLife(boolean[][] field) {
boolean[][] nextIteration = new boolean[field.length][field[0].length];
for (int x = 0; x < field.length; x++) {
for (int y = 0; y < field[x].length; y++) {
int neighbors = countNeighbors(field, x, y);
nextIteration[x][y] = field[x][y] ? (neighbors == 2 || neighbors == 3) : (neighbors == 3);
}
}
return nextIteration;
}
private int countNeighbors(boolean[][] field, int x, int y) {
int count = 0;
int xMin = Math.max(x - 1, 0);
int xMax = Math.min(x + 1, field.length - 1);
int yMin = Math.max(y - 1, 0);
int yMax = Math.min(y + 1, field[0].length - 1);
for (int i = xMin; i <= xMax; i++) {
for (int j = yMin; j <= yMax; j++) {
// Wir schließen i == x und j == y aus, weil wir sonst das Feld prüfen, dessen Nachbarn wir zählen.
if (field[i][j] && !(i == x && j == y)) {
count++;
}
}
}
return count;
}
private void sleep(long milliseconds) {
try {
Thread.sleep(milliseconds);
} catch (InterruptedException e) {
Thread.currentThread().interrupt();
}
}
}
Aufgabenstellung
Der Biologe Aristid Lindenmayer wandte kontextfreie Grammatiken an, um das Wachstum von Pflanzen zu beschreiben. Wir können in Kara ein einfaches Turtle-Graphiksystem simulieren, mit dem wir einige Beispiele von Lindenmayer-Systemn studieren können. Das Turtle-System kenne die Bewegungsbefehle der Kara-Umgebung: F für einen Schritt vorwärts sowie L und R für Links- beziehungsweise Rechtsdrehung um 90°. Diese drei Befehle können als Alphabet für Lindenmayer-Grammatiken benutzt werden. Ein Wort, das aus den Buchstaben dieses Alphabets gebildet wird, ist eine Wegbeschreibung für die Turtle. Eine einfache Grammatik besteht beispielsweise lediglich aus der folgenden Ersetzungsregel:
Diese Ersetzungsregel wird wiederholt auf ein beliebiges Wort angewendet, das aus den Buchstaben F, L und R besteht. Dabei wird jeweils jedes Vorkommen von F entsprechend der Ersetzungsregel ersetzt. Betrachten wir als Beispiel, wie die Regel zwei Mal auf das Wort "F" angewendet wird:
Die Länge der resultierenden Zeichenkette wächst exponentiell. Die Zeichenkette beschreibt eine immer detaillierter werdende Schneeflockenkurve, wie sie in obersten Abbildung dargestellt ist. Programmieren Sie Kara so, dass er einfache Lindenmayer-Systeme anwenden und darstellen kann! Sie benötigen dazu eine Suche-/Ersetze-Regel, die angibt, wie die Zeichenkette generiert werden soll, sowie Wort, das als Ausgangspunkt für die Ersetzungen dient. Ihr Programm muss die Ersetze-Regel auf dieses Wort mehrmals anwenden und die dabei entstehende Zeichenkette schliesslich "interpretieren", das heisst, die in ihr enthaltenen Befehle durch Kara ausführen lassen.
TODO! EXPLAIN
Einfache Lösung (kara.-Methoden)
myMainProgram executed in 1803744 millisecondsmyMainProgram executed in 1803.744 secondsmyMainProgram executed in 30.0624 minutes
import javakara.JavaKaraProgram;
public class Main extends JavaKaraProgram {
private static final int DEPTH = 6;
private static final int WIDTH = 731;
private static final int HEIGHT = 365;
public static void main(String[] args) {
new Main().run();
}
public void myMainProgram() {
world.setSize(WIDTH, HEIGHT);
kara.setPosition(0, HEIGHT - 1);
kara.setDirection(3);
sleep(5000);
String origin = "F";
String evolve = "FLFRFRFLF";
for (int i = 0; i < DEPTH; i++) {
origin = origin.replaceAll("F", evolve);
}
interpret(origin);
}
private void interpret(String instructions) {
kara.putLeaf();
for (int i = 0; i < instructions.length(); i++) {
switch (instructions.charAt(i)) {
case 'F':
kara.move();
if (!kara.onLeaf()) {
kara.putLeaf();
}
break;
case 'R':
kara.turnRight();
break;
case 'L':
kara.turnLeft();
break;
default:
break;
}
}
}
private void sleep(long milliseconds) {
try {
Thread.sleep(milliseconds);
} catch (InterruptedException e) {
Thread.currentThread().interrupt();
}
}
}
Optimierte Lösung
myMainProgram executed in 4154 millisecondsmyMainProgram executed in 4.154 secondsmyMainProgram executed in 0.069233 minutes
import javakara.JavaKaraProgram;
public class Main extends JavaKaraProgram {
private static final int DEPTH = 6;
private static final int HEIGHT = 365;
private static final int WIDTH = 2 * HEIGHT;
public static void main(String[] args) {
new Main().run();
}
public void myMainProgram() {
world.setSize(WIDTH, HEIGHT);
sleep(5000);
String origin = "F";
String evolve = "FLFRFRFLF";
for (int i = 0; i < DEPTH; i++) {
origin = origin.replaceAll("F", evolve);
}
interpret(origin);
}
private void interpret(String instructions) {
int x = 0;
int y = HEIGHT - 1;
int state = 1;
world.setLeaf(x, y, true);
/*
* 0 → Norden
* 1 → Osten
* 2 → Süden
* 3 → Westen
*/
for (int i = 0; i < instructions.length(); i++) {
switch (instructions.charAt(i)) {
case 'F':
switch (state) {
case 0:
if (y - 1 < 0) {
y = HEIGHT - 1;
} else {
y--;
}
break;
case 1:
if (x + 1 > WIDTH - 1) {
x = 0;
} else {
x++;
}
break;
case 2:
if (y + 1 > HEIGHT - 1) {
y = 0;
} else {
y++;
}
break;
case 3:
if (x - 1 < 0) {
x = WIDTH - 1;
} else {
x--;
}
break;
default:
break;
}
// world.setLeaf wirft keinen Fehler, wenn versucht wird
// ein Blatt auf ein Feld zu setzen, auf dem bereits eins ist.
world.setLeaf(x, y, true);
break;
case 'R':
state = (state + 1) % 4;
break;
case 'L':
if (state - 1 < 0) {
state = 3;
} else {
state -= 1;
}
break;
default:
break;
}
}
}
private void sleep(long milliseconds) {
try {
Thread.sleep(milliseconds);
} catch (InterruptedException e) {
Thread.currentThread().interrupt();
}
}
}
Gallerie
Lindenmayer-System mit Tiefe 1

Lindenmayer-System mit Tiefe 2

Lindenmayer-System mit Tiefe 3

Lindenmayer-System mit Tiefe 4

Lindenmayer-System mit Tiefe 5

Lindenmayer-System mit Tiefe 6

Eine höhere Tiefe würde außerhalb der maximalen Weltgröße (1000x1000) liegen. Schade...
Aufgabenstellung
Kara hat etwas gegen Unordnung. Daher beschliesst er, die Balken von Kleeblätter in seiner Welt zu sortieren. Ein mögliches Sortierverfahren ist BubbleSort.
Bubblesort funktioniert wie in der untenstehenden Abbildung dargestellt. Man "durchläuft" von oben nach unten die Welt und vergleicht immer zwei "Balken" von Kleeblättern miteinander. Wenn der untere kürzer ist als der obere, müssen sie vertauscht werden. Wenn zwei Balken vertauscht werden, muss nochmals vorne anfangen werden. Erst wenn bei einem Durchlauf aller Balken keine vertauscht werden mussten, sind sie sortiert.
TODO! EXPLAIN
Hinweis
Diese Algorithmus hat eine Zeitkomplexität von \( O(n^2) \), jegliche Optimisierung die man an diesem Algorithmus vornehmen könnte, die nicht die unterliegende Struktur verändert ist nicht relevant und wurde um die Verständlichkeit des Algorithmus zu maximieren, nicht vorgenommen.
Wer einen schnelleren Algorithmus schreiben möchte, sollte sich an QuickSort, MergeSort oder HeapSort wenden.
import javakara.JavaKaraProgram;
public class Main extends JavaKaraProgram {
public static void main(String[] args) {
new Main().run("F:\\Worlds\\KleeblattbalkenSortieren\\WorldOne.world");
}
public void myMainProgram() {
sleep(2500);
while (!isSorted()) {
for (int y = 0; y < world.getSizeY() - 1; y++) {
int current = getRowLength(y);
int next = getRowLength(y + 1);
if (current < next) {
clearRow(y + 1);
setRow(next, y);
setRow(current, y + 1);
}
}
}
}
private void clearRow(int y) {
for (int x = 0; x < world.getSizeX(); x++) {
world.setLeaf(x, y, false);
}
}
private void setRow(int x, int y) {
for (int i = 0; i < x; i++) {
world.setLeaf(i, y, true);
}
}
private boolean isSorted() {
for (int y = 0; y < world.getSizeY() - 1; y++) {
int current = getRowLength(y);
int next = getRowLength(y + 1);
if (current > next) {
return false;
}
}
return true;
}
private int getRowLength(int y) {
int counter = 0;
for (int x = 0; x < world.getSizeX(); x++) {
if (world.isLeaf(x, y)) {
counter++;
}
}
return counter;
}
private void sleep(long milliseconds) {
try {
Thread.sleep(milliseconds);
} catch (InterruptedException e) {
Thread.currentThread().interrupt();
}
}
}
Aufgabenstellung
Programmieren Sie JavaKara so, dass er ein "zweifarbiges" Mandelbrot-Fraktal zeichnet!
Was ist ein Mandelbrot-Fraktal?
Das Mandelbrot-Fraktal wurde von Benoit Mandelbrot entdeckt; sie repräsentieren die sogenannte Mandelbrot-Menge.
Um erklären zu können, nach welchen Vorschriften eine Mandelbrot-Menge berechnet wird, stellen wir uns folgendes vor: Ein Mandelbus startet innerhalb eines Kreises an einem Anfangspunkt und fährt nach bestimmten Vorschriften einer Strecke nach.
Gelangt der Mandelbus auf seiner Fahrstrecke ausserhalb des Kreises, so ist die Fahrroute ungültig und diese Fahrstrecke wird eliminiert, bleibt der Mandelbus hingegen immer im Kreis, so kann diese "Stecke" als gültig bezeichnet werden.
Die Fahrstrecke besteht aus Punkten. Den den aktuellen Anfangspunkt im Kreis bezeichnen wir als \( (a \mid b) \). Der Mandelbus startet im Punkt \( (a \mid b) \) und kommt durch unten dargestellte Berechnung zum nächsten Punkt. x und y sind die aktuellen Koordinaten des Mandelbusses, beim Start also a und b. \( (x[\text{neu}] \mid y[\text{neu}]) \) ist der nächste Punkt, zu dem sich der Mandelbus bewegt. Liegt nun einer dieser Punkte nach einer bestimmten Anzahl Berechnungen nicht mehr im Kreis, so ist die aktuelle Fahrroute ungültig.
Vorgehen für die Berechnung der Punkte in einer Mandelbrot-Menge:
Man nehme einen Punkt \( (a \mid b) \) innerhalb eines Kreises mit Radius 2 und rechne:
- \( x[\text{neu}] = x^2 - y^2 + a \) für die \( x \)-Koordinate des neuen Punktes.
- \( y[\text{neu}] = 2 \cdot x \cdot y + b \) für die \( y \)-Koordinate.
Nun rechne man nach obiger Vorschrift die Fahrstrecke des Mandelbusses. Für weitere Stationen des Mandelbusses wird der Punkt \( (x[\text{neu}] \mid y[\text{neu}]) \) immer zum aktuellen Punkt \( (x \mid y) \). So lässt sich dann der nächste Punkt als \( (x[\text{neu}] \mid y[\text{neu}]) \) berechnen.
Diesen Vorgang führen wir für jeden Punkt des Kreises ( = Anfangspunkte) 100 mal durch. Wenn nach diesen 100 Iterationen mit dem gewählten Anfangspunkt der aktuelle Punkt \( (x \mid y) \) nicht aus dem Kreis geraten ist, wird der zuvor gewählte Anfangspunkt eingefärbt.
Aufgabe
Schreiben Sie ein Programm, das in Kara's Welt Apfelmännchen zeichnet. Sie können wie folgt vorgehen:
- Schreiben Sie ein Hauptprogramm, das alle Felder in Kara's Welt durchläuft.
- Rechnen Sie dabei für jedes Feld die Koordinaten des Feldes um auf Koordinaten in einem Koordinatensystem mit \( (x_{\text{min}} = -2, x_{\text{max}} = 2, y_{\text{min}} = -2, y_{\text{max}} = 2) \).
- Wenden Sie die obige Rechenvorschrift an, um rauszufinden, ob der entsprechende Mandelbus den Kreis mit Radius 2 verlässt oder nicht.
- Falls der Bus den Kreis verlassen hat, legen Sie je ein Kleeblatt auf das entsprechende Feld in Kara's Welt
Wenn du es bis hierhin geschafft hast, Herzlichen Glückwunsch! Diese Aufgabe ist mit großem Abstand die schwerste in der Liste der internen JavaKara Aufgaben, selbst mit der gegebenen Hilfestellung der Aufgabenstellung.
Wir können anhand der Auflistung in der Aufgabenstellung jedoch Stückweise vorgehen und unsere Lösung Stück für Stück implementieren. Zunächst müssen wir jedes Feld der Welt durchlaufen, da wir zwei Koordinatenachsen besitzen, lässt sich dies mit einem doppelt genesteten for-Loop umsetzen. Wir gehen im äußeren Loop durch alle Spalten und im inneren durch alle Zeilen, die Reihenfolge ist jedoch eigentlich egal.
public void myMainProgram() {
// Wir könnten auch eine Welt in der `main`-Methode laden.
// WIDTH = 200
// HEIGHT = 200
world.setSize(WIDTH, HEIGHT);
for (int i = 0; i < WIDTH; i++) {
for (int j = 0; j < HEIGHT; j++) {
}
}
}
Als nächstes müssen wir die Koordinaten der Kara-Welt, welche links oben mit (0, 0) beginnt und rechts unten mit (WIDTH, HEIGHT) endet, in ein zentriertes, kartesisches Koordinatensystem umwandeln.
private double[] getCoordinate(int xPixel, int yPixel) {
double realMin = -2.0;
double realMax = 1.0;
double imagMin = -1.5;
double imagMax = 1.5;
double cx = realMin + ((double) xPixel / WIDTH) * (realMax - realMin);
double cy = imagMin + ((double) yPixel / HEIGHT) * (imagMax - imagMin);
return new double[]{cx, cy};
}
Beispielrechnung mit den Koordinaten (0, 0):
\[ cx = -2 + \frac{0}{200} \cdot 3 = -2 \] \[ cy = -1.5 + \frac{0}{200} \cdot 3 = -1.5 \]
Beispielrechnung mit den Koordinaten (200, 200) (Wenn WIDTH = 200 und HEIGHT = 200):
\[ cx = -2 + \frac{200}{200} \cdot 3 = 1 \] \[ cy = -1.5 + \frac{200}{200} \cdot 3 = 1.5 \]
Alle Koordinaten der Kara Welt werden somit auf die kartesischen Fläche übertragen. Daraus folgt folgendes Hauptprogramm:
public void myMainProgram() {
world.setSize(WIDTH, HEIGHT);
for (int i = 0; i < WIDTH; i++) {
for (int j = 0; j < HEIGHT; j++) {
double[] c = getCoordinate(i, j);
if (isInMandelbrotSet(c[0], c[1])) {
world.setLeaf(i, j, true);
}
}
}
}
Wir erstellen für jede Iteration der inneren Schleife einen Array, der die kartesischen Koordinaten speichert. Dann prüfen wir ob der Punkt mit diesen Koordinaten nach 100 iterationen divergiert (hier gegen unendlich geht) oder konvergiert (einen festen Wert annimmt).
Die Methode ist wie folgt aufgebaut:
private boolean isInMandelbrotSet(double cx, double cy) {
// Hier definieren wir den Real- und Imaginärteil der Koordinate.
double real = 0.0;
double imag = 0.0;
for (int i = 0; i < ITERATIONS; i++) {
// Wir quadrieren hier beide Komponeten der komplexen Zahl
double realSq = real * real;
double imagSq = imag * imag;
/*
* Und prüfen ob die Summe davon größer ist als ein gewisser Richtwert (hier 4.0).
* Wir können diese optimisierung vornehmen, da sich der "Mandelbus" spiralförmig bildet und
* wenn der Pfad der Koordinate einen gewissen Wert übersteigt, lässt sich mit sicherheit sagen,
* dass dieser Wert nicht mehr konvergiert. Das erspart uns bei der Berechnung sehr viele Iterationen.
*/
if (realSq + imagSq > 4.0) {
return false;
}
/*
* Hier schreiben wir berechneten Werte für die nächste Iteration auf die alten Variablen.
* Die Formeln stammen aus der Aufgabenstellung
* x[neu] = x^2 - y^2 + a
* y[neu] = 2 * x * y + b
*/
real = realSq - imagSq + cx;
imag = 2 * real * imag + cy;
}
return true;
}
Wenn der "Mandelbus" konvergiert, dann legen wir ein Blatt, wenn nicht, dann nicht.
Das gesammte Programm sieht so aus:
Hinweis
Es ist erwünscht mit den Variablen herumzuspielen, besonders mit
ITERATIONS, da die Anzahl der Iterationen bestimmt wie exakt die Mandelbrot-Menge konstruiert wird.
import javakara.JavaKaraProgram;
public class Main extends JavaKaraProgram {
private static final int WIDTH = 500;
private static final int HEIGHT = 500;
private static final int ITERATIONS = 1000;
/*
* Die Minimal- und Maximalwerte sind in dieser Version die genauen Grenzen der Mandelbrot-Menge
* Die obigen Werte sorgen für ein simpleres Mandelbrot-Fraktal, die Berechnungen sind aber dieselben.
*/
private static final double REAL_MIN = -2.00;
private static final double REAL_MAX = 0.47;
private static final double IMAG_MIN = -1.12;
private static final double IMAG_MAX = 1.12;
public static void main(String[] args) {
new Main().run();
}
public void myMainProgram() {
world.setSize(WIDTH, HEIGHT);
for (int i = 0; i < WIDTH; i++) {
for (int j = 0; j < HEIGHT; j++) {
double[] c = getCoordinate(i, j);
if (isInMandelbrotSet(c[0], c[1])) {
world.setLeaf(i, j, true);
}
}
}
}
private boolean isInMandelbrotSet(double cx, double cy) {
double real = 0.0;
double imag = 0.0;
for (int i = 0; i < ITERATIONS; i++) {
double realSq = real * real;
double imagSq = imag * imag;
if (realSq + imagSq > 4.0) {
return false;
}
real = realSq - imagSq + cx;
imag = 2 * real * imag + cy;
}
return true;
}
private double[] getCoordinate(int xPixel, int yPixel) {
double cx = REAL_MIN + ((double) xPixel / WIDTH) * (REAL_MAX - REAL_MIN);
double cy = IMAG_MIN + ((double) yPixel / HEIGHT) * (IMAG_MAX - IMAG_MIN);
return new double[]{cx, cy};
}
}
Aufabenstellung
Kara steht vor einem Baum, hinter dem sich ein Kleeblatt befindet. Kara soll um den Baum herumgehen, das Kleeblatt aufnehmen, es einen Schritt weiter ablegen, einen Schritt vorgehen und sich umdrehen.
import javakara.JavaKaraProgram;
public class Main extends JavaKaraProgram {
public static void main(String[] args) {
new Main().run("F:\\Worlds\\Extern\\Aufgabe1.world");
}
public void myMainProgram() {
kara.turnLeft();
kara.move();
kara.turnRight();
kara.move();
kara.move();
kara.turnRight();
kara.move();
kara.turnLeft();
kara.removeLeaf();
kara.move();
kara.putLeaf();
kara.move();
kara.turnLeft();
kara.turnLeft();
}
}
Aufgabenstellung
Kara steht vor einem Baum, hinter dem sich ein Kleeblatt befindet. Kara soll um den Baum herumgehen, das Kleeblatt aufnehmen, es einen Schritt weiter ablegen, einen Schritt vorgehen und sich umdrehen (wie auf dem Arbeitsblatt „Das erste Java-Programm“).
import javakara.JavaKaraProgram;
public class Main extends JavaKaraProgram {
public static void main(String[] args) {
new Main().run("F:\\Worlds\\Extern\\Aufgabe1.world");
}
public void myMainProgram() {
this.bypassTree();
kara.removeLeaf();
kara.move();
kara.putLeaf();
kara.move();
this.turnAround();
}
private void turnAround() {
kara.turnLeft();
kara.turnLeft();
}
private void bypassTree() {
kara.turnLeft();
kara.move();
kara.turnRight();
kara.move();
kara.move();
kara.turnRight();
kara.move();
kara.turnLeft();
}
}
Aufgabenstellung
Kara steht vor einem Baum oder nicht. Wenn nicht, soll er einfach einen Schritt weitergehen oder ansonsten um den einzelnen Baum herumgehen.
import javakara.JavaKaraProgram;
public class Main extends JavaKaraProgram {
public static void main(String[] args) {
new Main().run();
}
public void myMainProgram() {
if (kara.treeFront()) {
this.bypassTree();
} else {
kara.move();
}
}
private void bypassTree() {
kara.turnLeft();
kara.move();
kara.turnRight();
kara.move();
kara.move();
kara.turnRight();
kara.move();
kara.turnLeft();
}
}
Aufgabenstellung
Version 1: Kara steht vor einer Reihe von Kleeblättern, an deren Ende ein Baum steht. Die Kleeblattreihe kann Lücken haben. Kara soll alle Kleeblätter aufsammeln. Version 2: Kara soll die Kleeblattreihe invertieren, d.h. wenn er auf einem Kleeblatt steht, soll er es aufnehmen; wenn er keines vorfindet, soll er eines ablegen.
Version 1:
public void myMainProgram() {
while (!kara.treeFront()) {
this.pickUpLeaf();
kara.move();
}
this.pickUpLeaf();
}
private void pickUpLeaf() {
if (kara.onLeaf()) {
kara.removeLeaf();
}
}
Version 2:
public void myMainProgram() {
while (!kara.treeFront()) {
invertLeaf();
kara.move();
}
invertLeaf();
}
private void invertLeaf() {
if (kara.onLeaf()) {
kara.removeLeaf();
} else {
kara.putLeaf();
}
}
Aufgabenstellung
Kara soll ein Kleeblatt finden, das sich in der gleichen Zeile (oder Spalte) befindet wie er selbst. Zwischen ihm und dem Kleeblatt können Bäume stehen, wobei nie zwei Bäume direkt nebeneinander stehen. Schreibe das Programm mit der Methode
bypassTree().
public void myMainProgram() {
while (!kara.onLeaf()) {
if (kara.treeFront()) {
this.bypassTree();
} else {
kara.move();
}
}
}
private void bypassTree() {
kara.turnLeft();
kara.move();
kara.turnRight();
kara.move();
kara.move();
kara.turnRight();
kara.move();
kara.turnLeft();
}
Aufgabenstellung
Kara soll ein Kleeblatt finden, das sich in der gleichen Zeile (oder Spalte) befindet wie er selbst. Zwischen ihm und dem Kleeblatt können Bäume stehen, wobei mehrere Bäume hintereinander stehen können. Schreibe das Programm mit einer Methode
bypassTrees().
public void myMainProgram() {
while (!kara.onLeaf()) {
if (kara.treeFront()) {
this.bypassTrees();
} else {
kara.move();
}
}
}
private void bypassTrees() {
kara.turnLeft();
kara.move();
kara.turnRight();
do {
kara.move();
} while (kara.treeRight());
kara.turnRight();
kara.move();
kara.turnLeft();
}
Aufgabenstellung
Kara sucht das Ende eines einfachen Labyrinths bestehend aus Bäumen, wobei keine Löcher in den Baumreihen auftreten. Das Ende des Labyrinths ist eine „Sackgasse“.
public void myMainProgram() {
while (true) {
if (!kara.treeLeft()) {
kara.turnLeft();
kara.move();
} else if (!kara.treeRight()) {
kara.turnRight();
kara.move();
}
if (kara.treeFront() && kara.treeLeft() && kara.treeRight()) {
return;
}
kara.move();
}
}
Aufgabenstellung
Kara bewacht eine zusammenhängende Fläche, die durch Bäume begrenzt ist. Er soll endlos außen an den „Wänden“ aus Bäumen entlang laufen. Variante: Er soll zuerst zu seiner Fläche und dann erst endlos darum herum laufen.
public void myMainProgram() {
while (true) {
if (kara.treeFront()) {
kara.turnLeft();
} else {
if (kara.treeRight()) {
kara.move();
} else {
kara.turnRight();
kara.move();
}
}
}
}
Aufgabenstellung
Kara spielt Pacman: Er steht auf dem ersten Kleeblatt einer langen Spur von Kleeblättern, die vor einem Baum endet. Er soll alle Kleeblätter auffressen. Schwierige Variante: Die Kleeblattspur verläuft zwischen Bäumen und das Ende der Spur wird durch einen Pilz markiert.
X. Aufgabe
if-Statements
In der Programmierung werden wir oft mit Situationen konfrontiert, in denen wir abhängig einer oder mehreren Variablen, Entscheidungen treffen müssen. Ein Programm muss in der Lage sein, unterschiedliche Aktionen basierend auf bestimmten Bedingungen auszuführen. Hierfür verwenden wir Kontrollstrukturen wie das
if-Statement, welches eine der grundlegendsten Kontrollstrukturen in Java und vielen anderen Programmiersprachen darstellt.
Grundlegende Syntax
Die einfachste Form eines if-Statements in Java sieht folgendermaßen aus:
if (bedingung) {
// Code, der ausgeführt wird, wenn die Bedingung `true` ist
}
Hinweis
Ein
if-Statement prüft implizit ob die Bedingungtrueist.if (bedingung == true) {}Hat dieselbe Bedeutung wie
if (bedingung) {}
Die bedingung muss einen booleschen Wert (true oder false) enthalten. Wenn die Bedingung zu true ausgewertet wird, wird der Code innerhalb der geschweiften Klammern ausgeführt. Wenn die Bedingung false ergibt, wird dieser Code übersprungen.
if-else Statement
Mit einem if-else-Statement können wir eine alternative Ausführung festlegen, falls die Bedingung false ergibt:
if (bedingung) {
// Code, der ausgeführt wird, wenn die Bedingung `true` ist
} else {
// Code, der ausgeführt wird, wenn die Bedingung `false` ist
}
else-if Statement
Wenn wir mehrere Bedingungen prüfen möchten, können wir else if verwenden:
if (bedingung1) {
// Code, der ausgeführt wird, wenn bedingung1 `true` ist
} else if (bedingung2) {
// Code, der ausgeführt wird, wenn bedingung1 `false` und bedingung2 `true` ist
} else {
// Code, der ausgeführt wird, wenn beide Bedingungen `false` sind
}
Hier wird jede Bedingung der Reihe nach geprüft. Sobald eine Bedingung true ergibt, wird der zugehörige Code ausgeführt und alle nachfolgenden Bedingungen werden übersprungen.
Geschachtelte if-Statements
if-Statements können auch geschachtelt werden:
if (äußereBedingung) {
if (innereBedingung) {
// Code, der ausgeführt wird, wenn beide Bedingungen true sind
}
}
Vergleichsoperatoren
Für die Bedingungen in if-Statements werden oft Vergleichsoperatoren verwendet:
| Operator | Bedeutung |
|---|---|
== | Gleichheit |
!= | Ungleichheit |
> | Größer als |
< | Kleiner als |
>= | Größer oder gleich |
<= | Kleiner oder gleich |
Hinweis
Bei Vergleichen von Objekten mit
==wird die Referenzgleichheit geprüft, nicht die inhaltliche Gleichheit. Um den Inhalt von Objekten zu vergleichen, sollte dieequals()-Methode verwendet werden.
String str1 = "Hallo";
String str2 = "Hallo";
String str3 = new String("Hallo");
// Vergleicht Referenzen
if (str1 == str2) { // true, da beide auf den gleichen String-Pool-Eintrag verweisen
System.out.println("str1 und str2 haben die gleiche Referenz");
}
if (str1 == str3) { // false, da str3 ein neues Objekt im Heap ist
System.out.println("Dies wird nicht ausgegeben");
}
// Vergleicht Inhalte
if (str1.equals(str3)) { // true, da der Inhalt gleich ist
System.out.println("str1 und str3 haben den gleichen Inhalt");
}
Logische Operatoren
Um komplexere Bedingungen zu erstellen, können logische Operatoren verwendet werden:
| Operator | Bedeutung |
|---|---|
&& | Logisches UND (beide Bedingungen müssen true sein) |
|| | Logisches ODER (eine der Bedingungen muss true sein) |
! | Logisches NICHT (negiert den Wert) |
int alter = 25;
boolean hatFührerschein = true;
if (alter >= 18 && hatFührerschein) {
System.out.println("Die Person darf Auto fahren");
}
if (alter < 18 || !hatFührerschein) {
System.out.println("Die Person darf nicht Auto fahren");
}
Kurzschluss-Auswertung
Java verwendet "kurzschluss"-Operatoren. Das bedeutet, dass bei && die zweite Bedingung nur geprüft wird, wenn die erste Bedingung true ist. Bei || wird die zweite Bedingung nur geprüft, wenn die erste Bedingung false ist.
if (objekt != null && objekt.istGültig()) {
// objekt.istGültig() wird nur aufgerufen, wenn objekt nicht null ist
}
Der ternäre Operator
Eine Kurzform für einfache if-else-Statements ist der ternäre Operator:
// Syntax: bedingung ? ausdruck1 : ausdruck2
String status = (alter >= 18) ? "erwachsen" : "minderjährig";
Dies entspricht:
String status;
if (alter >= 18) {
status = "erwachsen";
} else {
status = "minderjährig";
}
Blocklose if-Statements
Wenn ein if-Statement nur eine einzige Anweisung enthält, können die geschweiften Klammern weggelassen werden:
if (bedingung)
eineAnweisung(); // Nur diese Anweisung gehört zum if-Block
// Hier beginnt wieder der normale Programmfluss
Hinweis
Obwohl blocklose
if-Statements syntaktisch korrekt sind, können sie zu schwer lesbarem Code und versteckten Fehlern führen. Es wird generell empfohlen, immer geschweifte Klammern zu verwenden, um den Code-Block klar abzugrenzen.
Übungsbeispiel: Studenten-Notensystem
Hier ist ein Beispiel für die Verwendung von if-Statements in einem einfachen Notensystem:
public class Notensystem {
public static void main(String[] args) {
int punkte = 78;
char note;
if (punkte >= 90) {
note = 'A';
} else if (punkte >= 80) {
note = 'B';
} else if (punkte >= 70) {
note = 'C';
} else if (punkte >= 60) {
note = 'D';
} else {
note = 'F';
}
System.out.println("Mit " + punkte + " Punkten erhält der Student die Note: " + note);
// Verwendung des ternären Operators für die Bewertung "bestanden/nicht bestanden"
String ergebnis = (punkte >= 60) ? "bestanden" : "nicht bestanden";
System.out.println("Der Student hat " + ergebnis);
}
}
Fehler und Best Practices
Häufige Fehler
-
Verwechslung von
=und==:// Falsch - weist den Wert zu, anstatt zu vergleichen if (x = 5) { ... } // Richtig - vergleicht den Wert if (x == 5) { ... } -
Vergessen von Klammern bei mehreren Anweisungen:
// Falsch - nur die erste Anweisung gehört zum if-Block if (x > 5) System.out.println("x ist größer als 5"); x = 5; // Diese Zeile wird immer ausgeführt! // Richtig if (x > 5) { System.out.println("x ist größer als 5"); x = 5; }
Best Practices
-
Immer geschweifte Klammern verwenden, auch für einzeilige Blöcke.
-
Bedingungen klar und lesbar formulieren.
-
Komplexe Bedingungen in kleinere, benannte Teile aufteilen:
// Komplex und schwer lesbar if (alter >= 18 && hatFührerschein && !istGefahrenquelle && fahrzeugVerfügbar) { ... } // Besser lesbar boolean darfFahren = alter >= 18 && hatFührerschein; boolean istSicher = !istGefahrenquelle && fahrzeugVerfügbar; if (darfFahren && istSicher) { ... } -
Vermeiden von tief geschachtelten
if-Statements - sie machen den Code schwer lesbar. Es ist besser frühe Returns oder das Extrahieren von Methoden zu verwenden.
Zusammenfassung
if-Statements sind ein grundlegendes Element der Programmierung, das es uns ermöglicht, Entscheidungen basierend auf bestimmten Bedingungen zu treffen. In Java können wir if, else if und else verwenden, um verschiedene Bedingungen zu prüfen und unterschiedliche Aktionen auszuführen.
Anhänge
Alle kara. Befehle
| Befehl | Funktion | Rückgabetyp |
|---|---|---|
kara.move() | Kara bewegt sich ein Feld nach vorne. | !boolean |
kara.turnRight() | Kara dreht sich um $90^{\circ}$ nach rechts. | !boolean |
kara.turnLeft() | Kara dreht sich um $90^{\circ}$ nach links. | !boolean |
kara.putLeaf() | Kara setzt auf das Feld, auf dem er sich gerade befindet ein Blatt. | !boolean |
kara.removeLeaf() | Kara entfernt ein Blatt auf dem Feld auf dem er sich gerade befindet. | !boolean |
kara.treeFront() | Erkennt ob ein Baum vor Kara steht. | boolean |
kara.treeRight() | Erkennt ob ein Baum rechts neben Kara steht. | boolean |
kara.treeLeft() | Erkennt ob ein Baum links neben Kara steht. | boolean |
kara.mushroomFront() | Erkennt ob ein Pilz vor Kara steht. | boolean |
kara.onLeaf() | Erkennt ob sich Kara auf einem Blatt befindet. | boolean |
kara.setPosition(int x, int y) | Positioniert Kara vom Ursprung (links oben in der Welt) aus auf die Koordinaten x und y. Zu beachten ist, dass die Welt mit null indiziert ist, d.h. Dass das n-te Feld den Index n - 1 hat, um Kara also auf das Feld in der fünften Spalte und der zweiten Zeile zu setzen müsste der Befehl kara.setPosition(4, 1) lauten. | !void |
kara.setDirection(int x) | Richtet Kara in die verschiedenen Himmelsrichtungen aus, dabei dient der Parameter x als Index für die vier verschiedenen Himmelsrichtungen:kara.setDirection(0) - Nordkara.setDirection(1) - Westkara.setDirection(2) - Südkara.setDirection(3) - Ost | !void |
kara.getPosition() | Gibt die aktuelle Position von Kara als Point-Objekt zurück. Die Koordinaten können über getPosition().x und getPosition().y abgerufen werden. | !Point |
kara.inspect() | Gibt einen String mit Informationen über Kara zurück, der Name, Position und Blickrichtung enthält. | String |
kara.toString() | Gibt einen String mit Informationen über Kara zurück, ähnlich wie inspect(). Format: "Kara: {x => X, y => Y, direction => DIRECTION}" oder "Kara: undefined" falls Kara nicht in der Welt existiert. | String |
kara.to_s() | Alias für toString(). Gibt einen String mit Informationen über Kara zurück. | String |
Hinweis
Die Befehle
kara.inspect(),kara.toString()undkara.to_s()geben alleKara: {x => 0, y => 0, direction => east}zurück, wenn Kara nicht in der Welt ist.
Alle world. Befehle
| Befehl | Funktion | Rückgabetyp |
|---|---|---|
world.clearAll() | Entfernt alle Objekte aus der Welt. | void |
world.getSizeX() | Gibt die Breite der Welt (Anzahl der Spalten) zurück. | int |
world.getSizeY() | Gibt die Höhe der Welt (Anzahl der Zeilen) zurück. | int |
world.isEmpty(int x, int y) | Prüft, ob das Feld an Position (x, y) leer ist (kein Objekt enthält). | boolean |
world.isLeaf(int x, int y) | Prüft, ob sich ein Blatt an Position (x, y) befindet. | boolean |
world.isMushroom(int x, int y) | Prüft, ob sich ein Pilz an Position (x, y) befindet. | boolean |
world.isTree(int x, int y) | Prüft, ob sich ein Baum an Position (x, y) befindet. | boolean |
world.setLeaf(int x, int y, boolean value) | Setzt oder entfernt ein Blatt an Position (x, y), abhängig vom boolean-Wert (true=setzen, false=entfernen). | !void |
world.setMushroom(int x, int y, boolean value) | Setzt oder entfernt einen Pilz an Position (x, y), abhängig vom boolean-Wert (true=setzen, false=entfernen). | !void |
world.setTree(int x, int y, boolean value) | Setzt oder entfernt einen Baum an Position (x, y), abhängig vom boolean-Wert (true=setzen, false=entfernen). | !void |
world.setSize(int width, int height) | Ändert die Größe der Welt auf die angegebene Breite und Höhe. (Zwischen 1 und 1000) | !void |
Alle tools. Befehle
| Befehl | Funktion | Rückgabetyp |
|---|---|---|
tools.sleep(int milliseconds) | Pausiert die Ausführung des Programms für die angegebene Zeit in Millisekunden. | !void |
tools.checkState() | Überprüft den aktuellen Thread-Zustand. Wird intern verwendet, um die Ausführung zu steuern. | void |
tools.println(String message) | Gibt die angegebene Nachricht in der Konsole aus. | void |
tools.random(int max) | Erzeugt eine Zufallszahl zwischen 0 und dem angegebenen Maximalwert (inklusive). | !int |
tools.showMessage(String message) | Zeigt die angegebene Nachricht in einem Dialog-Fenster an. | void |
tools.stringInput(String prompt) | Öffnet einen Dialog zur Eingabe von Text. Der Parameter ist die Aufforderung, die im Dialog angezeigt wird. | String |
tools.intInput(String prompt) | Öffnet einen Dialog zur Eingabe einer ganzen Zahl. Gibt Integer.MIN_VALUE zurück, wenn keine gültige Zahl eingegeben wurde. | !int |
tools.doubleInput(String prompt) | Öffnet einen Dialog zur Eingabe einer Dezimalzahl. Gibt Double.MIN_VALUE zurück, wenn keine gültige Zahl eingegeben wurde. | !double |